De van Zuijlen-projectie

Hieronder volgt mijn originele uitleg van de `van Zuijlen'-projectie, zoals verschenen in de Metaphoon

Eindelijk! Hierbij zal ik onthullen hoe de projectie werkt waarin de kaart van Metaphoor vanaf nu per decreet (van mij, dus) staat afgebeeld. Ten eerste is op de kaart¹ al te zien dat de schaal één op honderd miljoen is. De grootte van de landen is daarmee ongeveer hetzelfde als op de allereerste kaarten. Deze schaal is alleen geldig op de evenaar. De projectie is namelijk niet lengtegetrouw: Op hogere breedten zijn de breedtecirkels uitgerekt. Op de kaart zijn bovendien twee breedtecirkels te zien: die van 60° en de evenaar.

Hoe zit de projectie nu in elkaar? Meetkundig gezien is het een projectie van de bol op een cilinder waarvan de as noord-zuid loopt, en die om de bol heen zit. Bij elk punt A op de bol wordt het punt A' gevonden dat precies aan de andere kant van de pool op de evenaar ligt. Punten op één meridiaan hebben dus dezelfde A'. Nu snijdt de lijn door A en A' de cilinder op twee plaatsen: In A', want daar raakt de cylinder de bol, en in P. P is nu de projectie van A op de kaart volgens de `van Zuijlen'-projectie (hij heeft ook nog een andere naam, maar die weet ik niet uit mijn hoofd). Noot: inmiddels ben ik er achter dat dit een variant is op de Gall Stereografische Projectie. Bij deze laatste snijdt de projectiecilinder de bol bij de 45° breedtecirkels. Er zijn ook andere varianten, met cilinders die de bol op andere breedtes snijden.

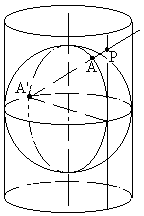
Op het plaatje zie je een poging om het allemaal nog eens duidelijk te tekenen.

Je kunt de projectie ook in formulevorm opschrijven. Dan luidt hij:

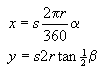
Waarbij x en y de coördinaten op de kaart zijn, alpha en beta respectievelijk de breedte- en lengtegraad, r de straal van Metaphoor, 6399.93 km, en s de schaal, 1/100.000.000.

¹ Hier wordt de A4-kaart zoals afgebeeld in de Metaphoon bedoeld. T.z.t. zal deze wellicht online beschikbaar komen.